¿Qué es un ángulo y por qué es mucho más que una figura geométrica?

-

El ángulo, esa figura tan familiar formada por dos líneas que se encuentran en un punto, es mucho más que una simple forma: es una herramienta esencial para comprender el mundo que nos rodea. Desde el giro de las manecillas del reloj hasta el diseño de mosaicos, los ángulos están por todas partes. 

¿Qué es realmente un ángulo?

El ángulo puede definirse de muchas formas, pero una muy significativa es la definición trigonométrica: un ángulo es la amplitud de rotación que describe un segmento rectilíneo que gira en torno a un punto fijo. Si ese giro es en sentido contrario a las agujas del reloj, el ángulo es positivo; si va en el mismo sentido, es negativo

Además, existen distintos tipos de ángulos: 

Por su amplitud:

  • Agudos: < 90°

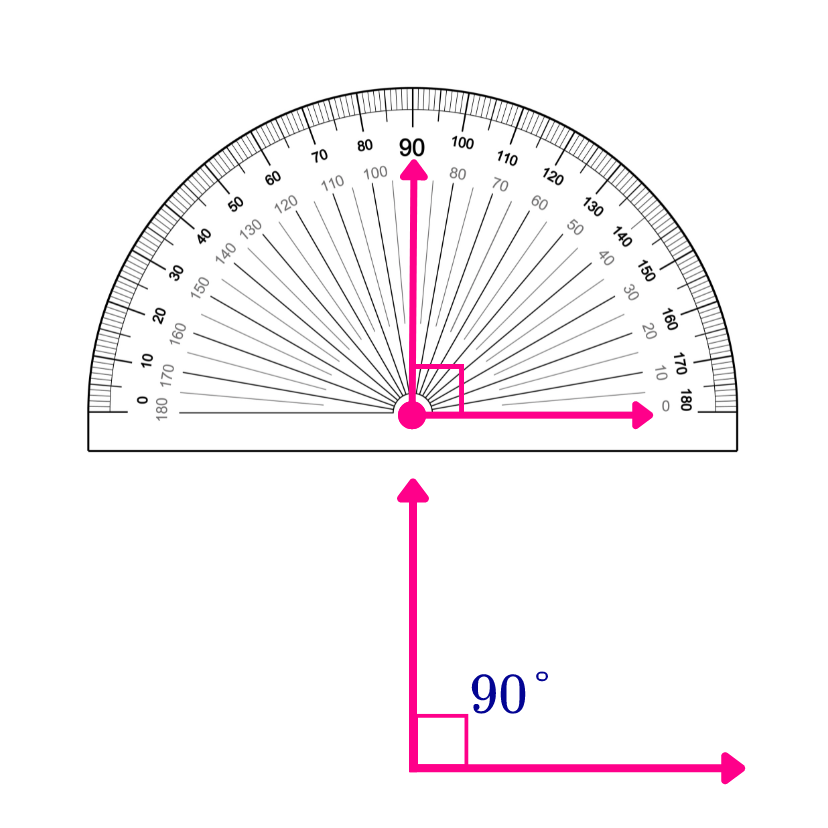
  • Rectos: = 90°

  • Obtusos: > 90° y < 180°

  • Llanos: = 180°

  • Cóncavos: entre 180° y 360°

  • Completos: = 360°

Por su posición: Consecutivos, adyacentes, opuestos por el vértice y correspondientes

Por su relación entre sí: Complementarios (suman 90°), suplementarios (suman 180°), conjugados (suman 360°), congruentes (miden lo mismo).

Instrumentos para medir ángulos

Para medir ángulos usamos principalmente el transportador, aunque también existen otros sistemas como el sistema centesimal, donde cada cuadrante se divide en 100 partes. Aunque esa última no se usa, es interesante conocer su existencia.

(Toda esta temática de ángulos está muy relacionada con la trigonometría, pero sobre ella ya hay una entrada en el blog, os invito a verla ;))

¿Cómo enseñar ángulos en Primaria?

Una enseñanza efectiva de los ángulos no puede basarse solo en definiciones o dibujos planos. Se deben utilizar: Modelos físicos (puertas, relojes, cartabones), tecnología educativa interactiva (juegos de arrastrar y medir), exploraciones prácticas, como medir el ángulo que forman nuestras piernas al caminar o los giros en un baile. 

Terminamos este punto recalcando lo siguiente; los ángulos no son solo parte del currículo, son parte de la realidad. Entenderlos, medirlos y relacionarlos con nuestro entorno ayuda a los niños a desarrollar habilidades espaciales, visuales y lógico-matemáticas. 

Un saludo, 

Ángel. 


Comentarios

Publicar un comentario

Entradas populares de este blog

Trigonometría: Medir lo innaccesible con razones y triángulos

-
Imagen
  ¿Cómo es posible medir la altura de un árbol sin escalarlo? ¿O calcular la distancia a una montaña sin caminar hasta ella? La respuesta está en una rama fascinante de las matemáticas: la trigonometría . Aunque su nombre pueda sonar intimidante, la trigonometría está presente en muchos aspectos de la vida cotidiana y tiene un poder impresionante: nos permite medir lo que no podemos tocar .  Bien, ¿Qué es la trigonometría?   La trigonometría es la parte de las matemáticas que estudia las relaciones entre los lados y los ángulos de los triángulos, especialmente los triángulos rectángulos.  En este contexto, surgen las razones trigonométricas , que no son más que relaciones constantes entre los lados de un triángulo rectángulo para un mismo ángulo.  Para un ángulo agudo en un triángulo rectángulo, estas son las razones más conocidas (respectivas razones tienen sus fórmulas que no he puesto pero pueden buscarlas): Seno (sen) : razón entre el cateto opuesto...
Leer más

Probabilidad y estadística para los niños/as en un centro escolar

-
Imagen
Para enfocar los contenidos de probabilidad y estadística dentro de una clase de didáctica de la medida en primaria, es útil integrarlos a través de actividades que vinculen la medición real  con la recolección, organización e interpretación de datos , así como con la incertidumbre y la predicción de resultados.  La intención de la publicación es enfocar estos contenidos a realizar una clase en primaria.  En cuanto a nociones de estadística , se pueden medir objetos del entorno, hacer tablas, pictogramas, diagrama de barras e incluso sacar conclusiones de datos recolectados. En cuanto a nociones de probabilidad: lanzar dados, monedas, ruletas, preguntar de manera que favorezca a la probabilidad "¿Qué es más probable que ocurra?" e incluso de manera que favorezca la frecuencia relativa; cuantas veces sucede algo comparado con el total.  Estas clases no solo son aplicables para la asignatura de matemáticas en primaria, puesto que en muchas asignaturas podemos lucha...
Leer más

Tablas de contingencia y sus aplicaciones en nuestra vida cotidiana

-
Imagen
 En la enseñanza y aprendizaje de las matemáticas, especialmente en la asignatura Didáctica de la Medida , muchas veces nos enfocamos en conceptos como longitud, masa, capacidad o tiempo. Sin embargo, para comprender verdaderamente cómo interpretamos y analizamos la información en la vida diaria, es esencial incluir herramientas estadísticas que nos permitan organizar y comparar datos de forma clara y significativa. Una de estas herramientas son las tablas de contingencia . ¿Qué es una tabla de contingencia?  Es una representación en forma de tabla que muestra la relación entre dos o más variables categóricas.  Por ejemplo, si en una clase se registran los tipos de instrumentos de medición que prefieren los estudiantes (regla, cronómetro) y se cruzan con su grado escolar, se puede construir una tabla que refleje estas preferencias por nivel educativo. ¿Por qué las tablas de contingencia son importantes?  Pues resulta que la enseñanza de la medida implica no solo apr...
Leer más